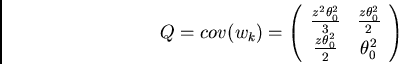Il Kalman Filter

Il Kalman Filter è una tecnica matematica che consente di stimare lo stato di un sistema in evoluzione (pur conoscendo la legge di evoluzione del sistema solo in modo approssimato) partendo da una serie di misure, affette da errore, prese a istanti successivi. La tecnica del Kalman Filter consente di combinare queste misure in modo che tutte contribuiscano alla determinazione dello stato del sistema ad ogni istante. Questa tecnica è stata sviluppata nel 1960 da R.E. Kalman [Kalman, 1960] e da allora ha avuto numerose applicazioni negli ambiti più disparati come, per esempio, l'ingegneria aerospaziale e l'economia.
Nel campo della fisica R. Frühwirth [Frühwirth, 1987] ha descritto un' applicazione del Kalman Filter al metodo di ricostruzione di tracce. Questo è stato in seguito usato per numerosi esperimenti di fisica delle particelle [Frühwirth et al., 1993] [Billoir, 1984] [Gravrilenko, 1996] e viene utilizzato in astronomia gamma per GLAST [Hernando, 1998].
E' possibile usare il Kalman Filter come metodo di "fit" delle tracce create dal passaggio di elettroni nel tracciatore di AGILE . Per far cio' si deve modellizzare il moto dell'elettrone in una proiezione dello strumento come un sistema che "evolve" dal primo piano in cui interagisce fino all'ultimo, considerando cioè i vari piani come istanti successivi dell'evoluzione in cui si acquisiscono informazioni su di esso. Le coordinate del vettore 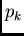, con il quale è descritto il sistema al generico piano k, possono essere la posizione dell'elettrone ( 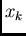) e la tangente dell'inclinazione del suo moto rispetto alla verticale ( 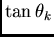) . La legge di evoluzione in questo modello è

$$p_{k}= F p_{k-1} + w_{k}$$ (33)

dove

$$F= \left(\begin{array}{cc} 1 & d \\ 0 & 1 \\ \end{array} \right)$$ (34)

rappresenta semplicemente la proiezione geometrica da un piano al successivo, d è la distanza tra i piani del tracciatore (1.6 cm), e 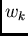rappresenta lo scostamento da questa proiezione dovuta allo scattering multiplo. Tale effetto è tradotto dalla matrice

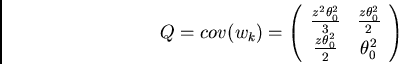$$Q = cov (w_{k}) = \left(\begin{array}{cc} \frac{z^{2}\theta... ...{z\theta_{0}^{2}}{2} & \theta_{0}^{2} \\ \end{array} \right)$$ (35)

dove 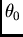rappresenta l'ampiezza dello scattering multiplo definita dall'equazione () a pagina . Essa dipende dall'energia dell'elettrone (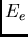 ), e dallo spessore (z) del piano attraversato.
Le quantità che formano il vettore 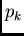sono state scelte in modo che l'evoluzione potesse essere descritta da una legge lineare, il che è fondamentale per l'applicabilità del Kalman Filter. L'incertezza delle nostre conoscenze dello stato del sistema può essere descritta da una matrice

$$C_{k}= cov (p_{k}-p_{k}^{true})$$ (36)

dove 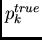contiene i valori reali del sistema al piano k.
Ad ogni piano si avrà una misura del passaggio della particella ( 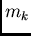), l'operazione di misura del sistema puo essere vista come un'operazione del tipo:

$$m_{k} = H p_{k} + \mu$$ (37)

dove H rappresenta la trasformazione di coordinate tra le quantità che rappresentano il vettore 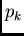e le quantità misurate. In questo caso

$$H = \left( \begin{array}{cc} 1 & 0 \\ \end{array} \right)$$ (38)

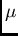è l'errore commesso nella misura. Quest'errore è descritto dalla matrice :

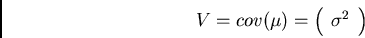$$V = cov( \mu ) = \left( \begin{array}{c} \sigma^{2} \\ \end{array} \right)$$ (39)