Ecco un esempio per chiarire i concetti esposti (vedi anche [Maybeck, 1979]). Si supponga di conoscere
esattamente
la posizione dell'elettrone al piano k-1, e che invece la stima
dell'inclinazione del suo
moto (
![]() ) sia affetta da errore. Se questo errore è
descrivibile in termini di una
distribuzione normale con varianza
) sia affetta da errore. Se questo errore è
descrivibile in termini di una
distribuzione normale con varianza ![]() , è possibile stabilire
la posizione dell'elettrone sul piano successivo in termini di probabilità di
presenza.
Questa sarà approssimativamente una gaussiana centrata nella posizione
, è possibile stabilire
la posizione dell'elettrone sul piano successivo in termini di probabilità di
presenza.
Questa sarà approssimativamente una gaussiana centrata nella posizione
![]() e con varianza
e con varianza
![]() .
.
A sua volta, una misura sul piano k può essere descritta
da una distribuzione gaussiana con picco in ![]() e varianza
e varianza
![]() .
.
È noto che due gaussiane (con medie in ![]() e varianze
e varianze
![]() ) derivate da stime indipendenti
possono essere combinate in una distribuzione con varianza :
) derivate da stime indipendenti
possono essere combinate in una distribuzione con varianza :
Il calcolo del Kalman filter sfrutta gli stessi principi estendendoli però a variabili con più dimensioni. Nel formalismo matriciale lo stato del sistema sul piano k vale:
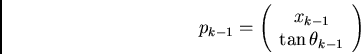
A questa è associata una matrice di covarianza :

dove ![]() è stato inserito solo per rendere la matrice invertibile,
ma può essere pensato piccolo a piacere. Partendo da queste informazioni è
possibile fare una previsione sullo stato al piano k :
è stato inserito solo per rendere la matrice invertibile,
ma può essere pensato piccolo a piacere. Partendo da queste informazioni è
possibile fare una previsione sullo stato al piano k :
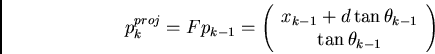
la matrice di covarianza proiettata sul piano k diventa :
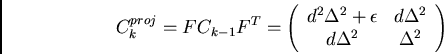
dove, per semplicità , si è posto Q =0. In questa matrice gli
elementi
sulla diagonale esprimono (in termini di varianza) l'incertezza rispettivamente
sulla posizione e sulla direzione.
Se sul piano k viene presa una misura ![]() , si ottiene :
, si ottiene :
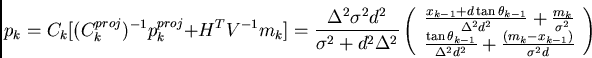
Il primo elemento di ![]() è uguale alla (2.16), mentre il secondo
esprime l'analogo risultato per
è uguale alla (2.16), mentre il secondo
esprime l'analogo risultato per
![]() .
L'incertezza legata a queste stime è contenuta in :
.
L'incertezza legata a queste stime è contenuta in :
![\begin{displaymath}
C_{k} = [ (C_{k}^{proj})^{-1} + H^{T} V^{-1} H ]^{-1} =
\fr...
...ay}{cc}
\par d^{2} & d \\
\par d & 1
\par\end{array} \right)
\end{displaymath}](img182.png)
nella quale il primo elemento della diagonale principale è uguale a (2.15).