



Next: La rivelazione di fotoni
Up: Il moto degli elettroni
Previous: Perdita di energia degli
Contents
Lo scattering degli elettroni
Il passaggio tra i piani del tracciatore altera, oltre che l'energia, anche la
direzione iniziale degli elettroni. Il moto di particelle cariche nella materia
è infatti influenzato anche da ripetute interazioni elastiche con i nuclei
atomici. In prima approssimazione queste collisioni sono descritte dalla formula
di Rutherford:
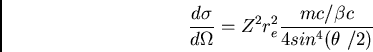 |
(12) |
dove
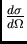 indica la sezione d'urto per unità di angolo
solido, e
indica la sezione d'urto per unità di angolo
solido, e 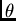 la deviazione dalla direzione originaria. A causa della
dipendenza da
la deviazione dalla direzione originaria. A causa della
dipendenza da
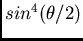 nel denominatore sono molto favorite le
collisioni con piccoli angoli di deviazione. Tuttavia l'effetto complessivo,
dovuto al passaggio attraverso un certo spessore di materia, è dato
dall'accumulo di queste piccole deviazioni e può essere sensibile.
nel denominatore sono molto favorite le
collisioni con piccoli angoli di deviazione. Tuttavia l'effetto complessivo,
dovuto al passaggio attraverso un certo spessore di materia, è dato
dall'accumulo di queste piccole deviazioni e può essere sensibile.
A seconda dello spessore di materia attraversato, si può dividere il processo
in tre classi [Leo, 1987], single scattering per materiali molto sottili
tali per cui la probabilità di più di uno scattering Coulombiano è
piccola, plural scattering quando il numero medio di collisioni è
minore di 20 e multiple scattering quando il numero di collisioni è
maggiore di 20 e la perdita di energia è piccola. In quest'ultimo caso, si
può trattare statisticamente il problema ottenendo una distribuzione di
probabilità per l'angolo di deviazione dipendente dallo spessore di materiale
attraversato.
Un calcolo rigoroso di tale effetto è stato sviluppato da Moliere ed è
valido per angoli 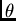 fino a 30 gradi con l'eccezione di elettroni lenti
(
fino a 30 gradi con l'eccezione di elettroni lenti
(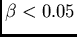 ) in elementi con alto Z.
) in elementi con alto Z.
Il calcolo di Moliere da la distribuzione dell'angolo polare sotto forma di una
serie:
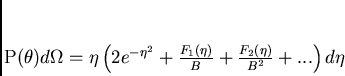 |
(13) |
in cui
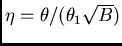 ,
,
mentre B è definito dall'equazione
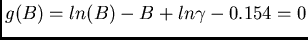 con
con
Le funzioni 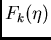 sono definite dall'integrale:
sono definite dall'integrale:
Questa distribuzione per piccoli angoli è approssimativamente una gaussiana,
ma ha significative code non gaussiane. Queste code sono dovute a singole
collissioni con parametri d'urto molto piccoli, e non ad una somma di piccole
deviazioni; perciò non possono essere trattate in semplici termini statistici.
Se si escudono questi urti "frontali" tra elettroni e nuclei, che comunque sono
poco probabili, la distribuzione di probabilità può essere messa nella forma
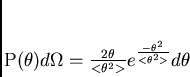 |
(14) |
Dove 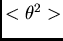 è il secondo momento della distribuzione. Paragonando la
è il secondo momento della distribuzione. Paragonando la
![[*]](file:/usr/lib/latex2html/icons/crossref.png) al primo termine della
al primo termine della ![[*]](file:/usr/lib/latex2html/icons/crossref.png) si può porre :
si può porre :
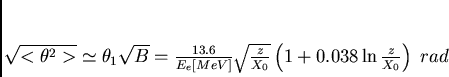 |
(15) |
dove 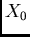 è la lunghezza di radiazione del materiale e z lo spessore.
è la lunghezza di radiazione del materiale e z lo spessore.
Spesso però è più utile usare la proiezione su di un piano della
deviazione angolare di scattering. Questa quantità è distribuita ancora in
modo gaussiano ma vale
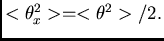
È interessante notare che anche lo spostamento spaziale che la particella
subisce attraversando il materiale a causa dello scattering multiplo si
distribuisce approssimativamente in modo gaussiano. Si può trovare che vale :
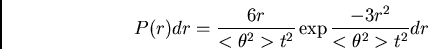 |
(16) |
dove r è lo spostamento e 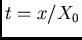 . è facilmente verificabile che
vale:
. è facilmente verificabile che
vale:




Next: La rivelazione di fotoni
Up: Il moto degli elettroni
Previous: Perdita di energia degli
Contents
Andrea Giuliani
2003-10-14
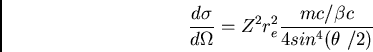
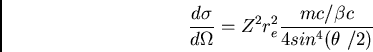
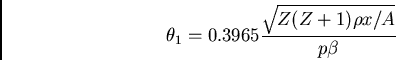
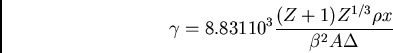
![\begin{displaymath}
F_k(\eta) = \frac{1}{k!} \int J_0 (\eta y) e^{\frac{-y^2}{4}} \left[
\frac{-y^2}{4} ln \frac{-y^2}{4} \right] ^k y dy
\end{displaymath}](img111.png)