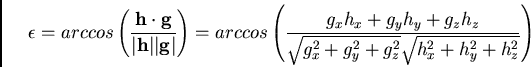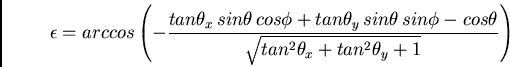Next: Ambiguità nell'associazione di tracce
Up: Errori nella misura della
Previous: Metodo di analisi
Contents
In questo metodo le proiezioni delle tracce nelle due viste
sono trattate indipendentemente. Si assume cioè che le proiezioni della bisettrice
tridimensionale delle tracce coincidano con le
bisettrici delle proiezioni delle tracce.
Questo vale solo in modo approssimato, l'errore commeso cresce
all'aumentare dell'angolo 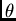 e all'aumentare dell'apertura della coppia.
Il metodo delle proiezioni è illustrato in figura
e all'aumentare dell'apertura della coppia.
Il metodo delle proiezioni è illustrato in figura ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
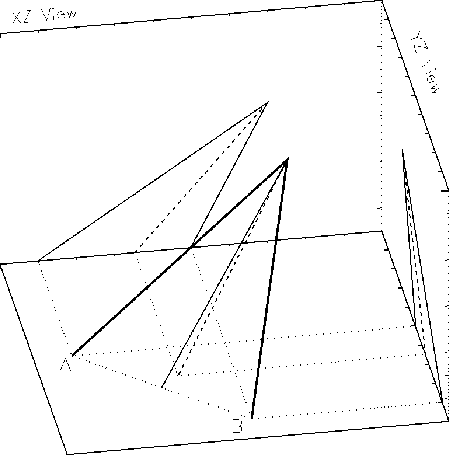
Figure:
Componendo le bisettrici delle proiezione nelle due viste si ottiene
una direzione tridimensionale (tratteggiata) diversa dalla vera bisettrice (solida).
 |
Le due bisettrici delle proiezioni delle tracce si
trovano facilmente ponendo:
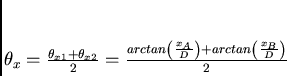 |
(64) |
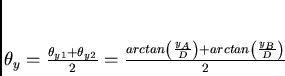 |
(65) |
Dove 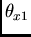 e
e 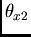 sono le inclinazioni
rispetto alla verticale delle due tracce
nella vista X e
sono le inclinazioni
rispetto alla verticale delle due tracce
nella vista X e 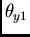 e
e 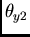 le inclinazioni nella vista Y.
le inclinazioni nella vista Y.
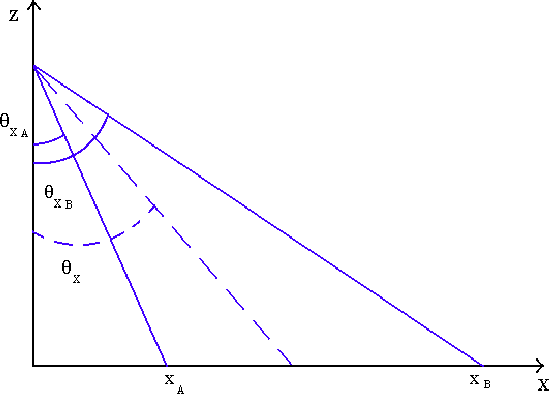
Figure:
Angoli definiti per le proiezioni delle tracce. Per il
piano YZ si avrebbe una figura analoga.
 |
Combinando 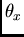 e
e 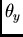 si ottiene una direzione (h) nello spazio tridimensionale,
é conveniente scrivere questa direzione come un vettore:
si ottiene una direzione (h) nello spazio tridimensionale,
é conveniente scrivere questa direzione come un vettore:
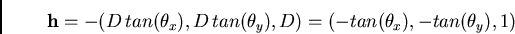 |
(66) |
Calcolando la
separazione tra la direzione di arrivo vera g e quella sbagliata h,
si ottiene l'errore che si commette usando questo metodo:
 |
(67) |
Quindi:
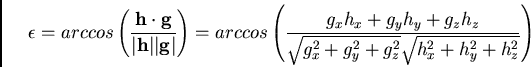 |
(68) |
L'ampiezza del errore commesso dipende, oltre che
dalla direzione di arrivo, dall'apertura della coppia e dalla sua orientazione
nello spazio.
La formula precedente scritta in termini dei 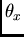 e
e 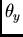 misurati e della direzione
di arrivo del fotone (
misurati e della direzione
di arrivo del fotone (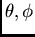 ) diventa:
) diventa:
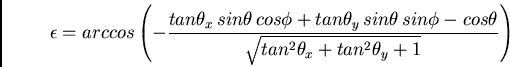 |
(69) |
Attraverso le equazioni (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) e (
) e (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) e
le relazioni (
) e
le relazioni (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) e (
) e (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) si può ricavare l'errore
) si può ricavare l'errore 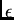 in funzione di
in funzione di 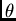 ,
, 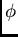 ,
, 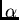 e
e 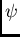 .
.
Nelle figure che seguono sono mostrati alcuni esempi della dipendenza di 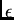 da
da 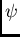 e da
e da 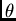 .
.
Figure:
Errore angolare nel metodo delle proiezioni in funzione dell'angolo di orientazione della coppia 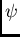 e per un'apertura della coppia di 12 gradi. Le curve si riferiscono a diverse direzioni d'incidenza con
e per un'apertura della coppia di 12 gradi. Le curve si riferiscono a diverse direzioni d'incidenza con
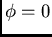 gradi.
gradi.
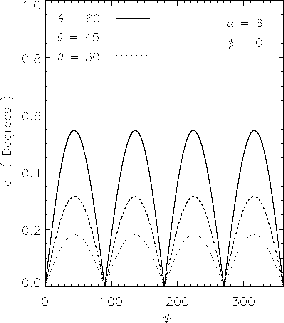 |
Figure:
Come per la figura precedente ma per 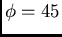 gradi.
gradi.
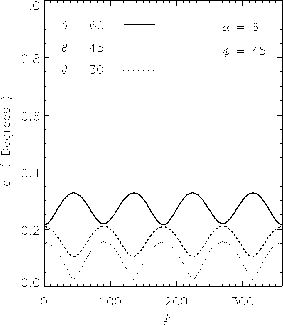 |
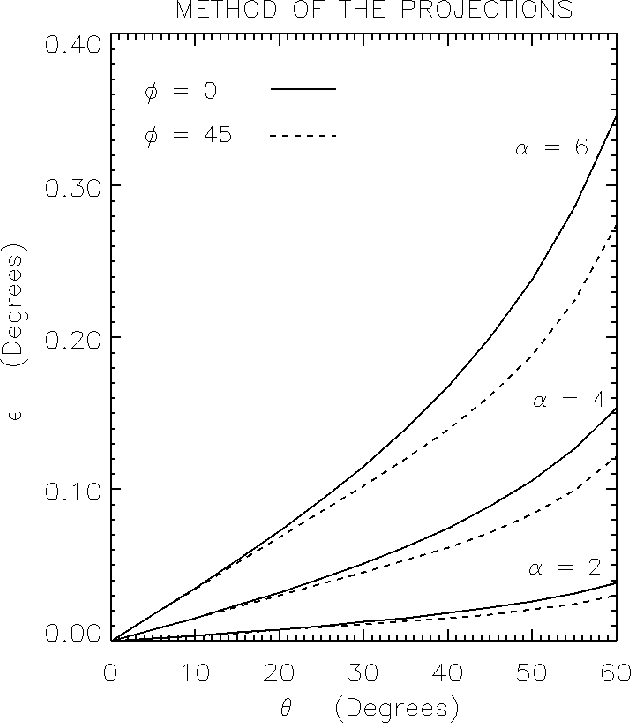
Figure:
Errore medio nel metodo delle proiezioni in funzione dell'angolo 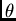 e per tre valori della
semiapertura
e per tre valori della
semiapertura 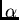 . Le curve continue sono per
. Le curve continue sono per 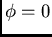 gradi e quella tratteggiate per
gradi e quella tratteggiate per 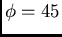 gradi.
Per differenti valori di
gradi.
Per differenti valori di 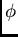 le curve sarebbero contenute tra questi due casi.
le curve sarebbero contenute tra questi due casi.
 |




Next: Ambiguità nell'associazione di tracce
Up: Errori nella misura della
Previous: Metodo di analisi
Contents
Andrea Giuliani
2003-10-14