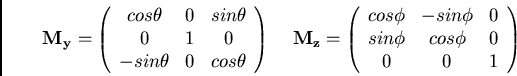Next: Metodo delle proiezioni
Up: Errori nella misura della
Previous: Errori nella misura della
Contents
Si prenda un sistema di riferimento solidale con il tracciatore, con
origine coincidente con il vertice della coppia 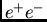 , con asse Z parallelo
all'asse di Z AGILE e con gli assi X e Y orientati parallelamente ai rispettivi
piani X e Y del tracciatore stesso (vedi figura
, con asse Z parallelo
all'asse di Z AGILE e con gli assi X e Y orientati parallelamente ai rispettivi
piani X e Y del tracciatore stesso (vedi figura ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
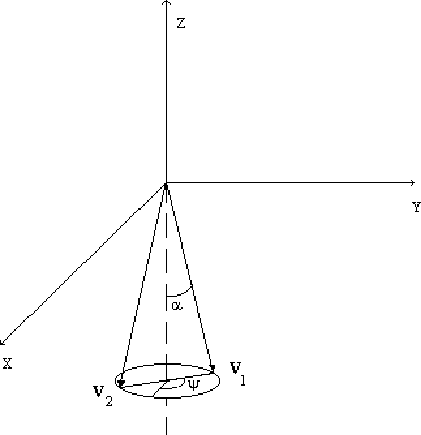
Figure:
Rappresentazione dei vettori che definiscono le direzioni della coppia di elettroni
per un fotone in asse.
 |
Se la direzione di arrivo g del fotone
coincide con l'asse Z è possibile descrivere le possibili orientazioni della
coppia di particelle con una coppia di vettori
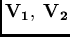 dati da :
dati da :
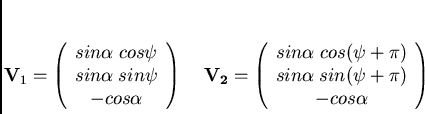 |
(58) |
Con 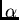 semiapertura della coppia. Variando
semiapertura della coppia. Variando 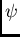 tra 0 e
tra 0 e  si ottengono
tutte le possibili orientazioni della coppia per un fissato
si ottengono
tutte le possibili orientazioni della coppia per un fissato 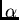 .
.
Figure:
Definizione degli angoli 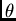 e
e 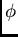 usati nella trattazione.
usati nella trattazione.
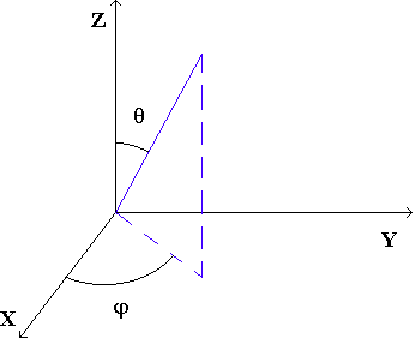 |
Se la direzione di arrivo del fotone é una generica direzione g' definita
dagli angoli 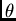 e
e 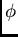 vale :
vale :
 |
(59) |
dove 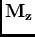 e
e 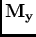 sono le matrici di rotazione intorno agli assi Z e Y :
sono le matrici di rotazione intorno agli assi Z e Y :
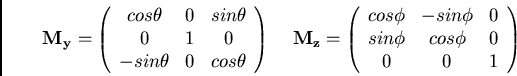 |
(60) |
Quindi la stessa trasformazione applicata ai vettori (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) da ancora una coppia
con apertura
) da ancora una coppia
con apertura 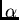 , la bisettrice delle quali é ora g'.
, la bisettrice delle quali é ora g'.
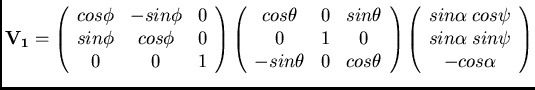 |
|
|
|
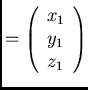 |
|
|
(61) |
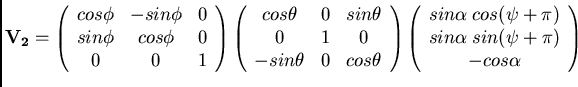 |
|
|
|
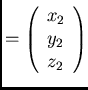 |
|
|
(62) |
I punti di intersezione delle traiettorie della coppia di elettroni con il secondo piano del tracciatore si
possono trovare facilmente
prolungando i vettori 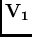 e
e 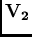 su un piano a distanza D dal origine, assumendo quindi D la distanza
tra due piani successivi. Le coordinate x e y di tali punti valgono:
su un piano a distanza D dal origine, assumendo quindi D la distanza
tra due piani successivi. Le coordinate x e y di tali punti valgono:
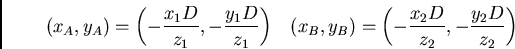 |
(63) |
Poiché nel tracciatore le informazioni X saranno date indipendentemente dalle informazioni Y, dopo la rivelazione
di un evento si disporrà delle coordinate 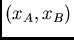 e delle coordinate
e delle coordinate 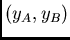 senza alcuna correlazione tra loro.
Questo vale indipendentemente dalla tecnica di fit usata per le tracce, l'unica differenza sta nel fatto che un metodo
"a due piani" userà come coordinate i centroidi delle misure prese sul secondo piano, mentre un metodo a più
piani, come il Kalman filter, correggerà la misura in base alle informazioni sui piani successivi.
Nei due paragrafi successivi si assumerà di disporre esattamente di
senza alcuna correlazione tra loro.
Questo vale indipendentemente dalla tecnica di fit usata per le tracce, l'unica differenza sta nel fatto che un metodo
"a due piani" userà come coordinate i centroidi delle misure prese sul secondo piano, mentre un metodo a più
piani, come il Kalman filter, correggerà la misura in base alle informazioni sui piani successivi.
Nei due paragrafi successivi si assumerà di disporre esattamente di 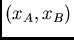 e
e 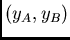 ,
ignorando gli errori
di misura. Nel paragrafo
,
ignorando gli errori
di misura. Nel paragrafo ![[*]](file:/usr/lib/latex2html/icons/crossref.png) saranno invece presentati gli effetti causati dalla risoluzione spaziale finita
in relazione alla misura della bisettrice delle tracce.
saranno invece presentati gli effetti causati dalla risoluzione spaziale finita
in relazione alla misura della bisettrice delle tracce.




Next: Metodo delle proiezioni
Up: Errori nella misura della
Previous: Errori nella misura della
Contents
Andrea Giuliani
2003-10-14