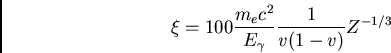 |
(18) |
Questo processo dipende dall'intensitá del campo elettrico nel punto in cui avviene. Per questo la sezione d'urto dipende, oltre che dall'energia del fotone primario, dal numero atomico Z del materiale e dalla distanza dal nucleo. Infatti maggiore é questa distanza e maggiore sará lo screening degli elettroni orbitali. L'influenza dello screening é determinata dalla quantitá :
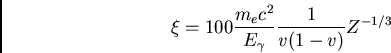 |
(18) |
dove
 |
(19) |
é la frazione di energia presa dal positrone. L'effetto di screening é maggiore per uno ![]() minore. Se
minore. Se ![]() lo screeening é trascurabile, mentre
lo screeening é trascurabile, mentre ![]() indica un completo screening. Per un dato valore di v,
indica un completo screening. Per un dato valore di v, ![]() diminuisce all'aumentare di
diminuisce all'aumentare di ![]() . Lo screening puó quindi essere considerato completo per ogni processo di produzione di coppie quando l'energia dell'fotone incidente é grande (
. Lo screening puó quindi essere considerato completo per ogni processo di produzione di coppie quando l'energia dell'fotone incidente é grande (
![]() ).
).
Si può definire una probabilitá differenziale di produzione di coppia
![]() tale per cui
tale per cui
![]() rappresenta la probabilitá per un fotone di energia
rappresenta la probabilitá per un fotone di energia ![]() che attraversa uno spessore dx
che attraversa uno spessore dx ![]() ) di produrre una coppia in cui l'elettrone ha un energia cinetica compresa tra
) di produrre una coppia in cui l'elettrone ha un energia cinetica compresa tra ![]() e
e ![]() . Assumendo che
. Assumendo che
![]() l'espressione teorica per
l'espressione teorica per ![]() é :
é :
in cui
![]() varia lentamente con
varia lentamente con ![]() e v. Nei casi limite di screening completo o di assenza di screening
e v. Nei casi limite di screening completo o di assenza di screening
![]() vale [Rossi, 1952]:
vale [Rossi, 1952]:
![\begin{displaymath}
G(E_{\gamma},v) = \left\{ \begin{array}{ll}
\left[v^2 + (1-...
...e c^2}-\frac{1}{2}\right] & \xi \gg 1 \\
\end{array} \right.
\end{displaymath}](img129.png) |
(21) |
Essendo G simmetrica tra v e 1-v, ![]() è complessivamente simmetrica per l'elettrone e il positrone. Integrando
è complessivamente simmetrica per l'elettrone e il positrone. Integrando ![]() in
in ![]() si ottiene la sezione d'urto totale, questo può essere fatto analiticamente solo per i due casi limite:
si ottiene la sezione d'urto totale, questo può essere fatto analiticamente solo per i due casi limite:
![\begin{displaymath}
\tau_{pair} = \left\{ \begin{array}{ll}
4 \alpha N \frac{Z^...
...}-\frac{109}{54}})\right] & \xi \gg 1 \\
\end{array} \right.
\end{displaymath}](img130.png) |
(22) |
per valori intermedi di ![]() bisogna valutare l'integrale numericamente. Per
bisogna valutare l'integrale numericamente. Per ![]() e quindi per
e quindi per ![]() elevate
elevate ![]() é circa costante.
é circa costante.
La produzione di coppie puó avvenire anche nel campo di un elettrone nucleare. L'analoga sezione d'urto che si ottiene da questa reazione é piú piccola di un fattore Z. Per tenere conto di questa interazione si puo' quindi sostituire nella formula precedente ![]() con Z(Z+1).
con Z(Z+1).
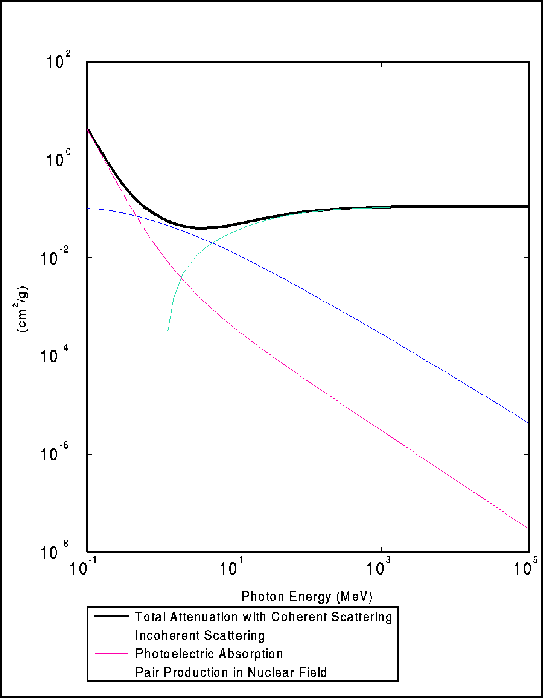
In figura ![]() é mostrata la sezione d'urto totale relativa al Tungsteno per
la produzione di coppie in funzione di
é mostrata la sezione d'urto totale relativa al Tungsteno per
la produzione di coppie in funzione di ![]() e in relazione agli altri principali processi di
assorbimento, lo scattering Compton e fotoelettrico. Al di sopra dell'energia di
soglia la probabilitá di assorbimento di un fotone per produzione di coppie
aumenta molto velocemente, fino a diventare il processo dominante per energie
maggiori di circa 10 MeV.
e in relazione agli altri principali processi di
assorbimento, lo scattering Compton e fotoelettrico. Al di sopra dell'energia di
soglia la probabilitá di assorbimento di un fotone per produzione di coppie
aumenta molto velocemente, fino a diventare il processo dominante per energie
maggiori di circa 10 MeV.
 |
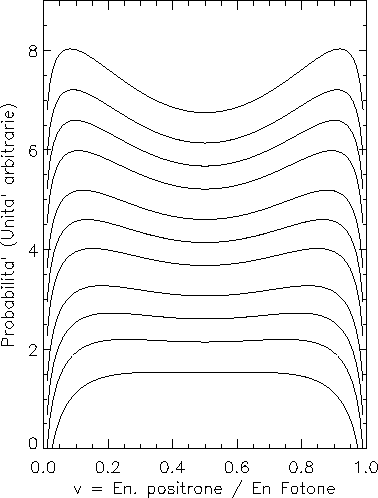
E' interessante studiare come l'energia del fotone si divida tra i due elettroni prodotti, questa informazione é contenuta in ![]() . In figura
. In figura ![]() é graficata
é graficata ![]() in funzione di v per diverse
in funzione di v per diverse ![]() . Va notato che il valore di v più probabile varia al variare dell'energia del fotone incidente, in particolare per alte energie é favorita una distribuzione assimmetrica dell'energia.
. Va notato che il valore di v più probabile varia al variare dell'energia del fotone incidente, in particolare per alte energie é favorita una distribuzione assimmetrica dell'energia.
 |