Mapping the matter distribution in the Galaxy

Figure 2.2: Simplified plan-view sketch of our galaxy showing regions of relative approach and recession with respect to the Sun [Kraus, 1986].

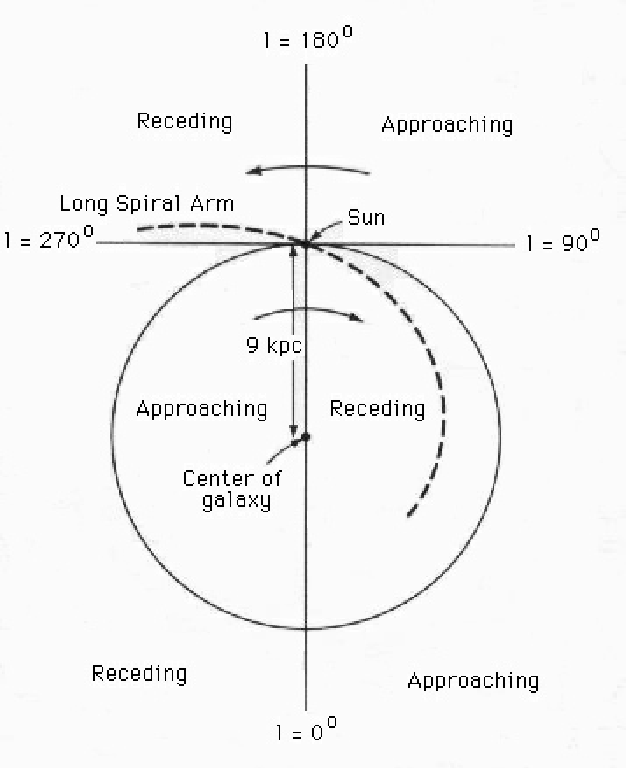Radio emission from the interstellar matter is dominated by emission lines of its constituents. The width of these lines, which are shifted by the Doppler effect, depends on both temperature and turbulence existing in the emitting clouds. Due to the optimal spectral resolution of radio receivers, the observation of lines at radio wavelengths allows to resolve the Doppler shift and to measure the radial velocity of the emitting matter. It is therefore possible to produce sky survey in which, for every direction, the emission is given as a function of the radial velocity with which the line is observed. The data cubes produced in this way are usually called velocity-resolved surveys. Velocity-resolved radio data, as for example the 21 cm survey, have proved to be a very important tool for studying the gas distribution in the spiral arms of our galaxy.
These surveys are very important because they allow to obtain a three-dimensional distribution of the medium which has generated the observed emission.

Figure 2.3: Geometric entities relevant in the computation. [Kraus, 1986]

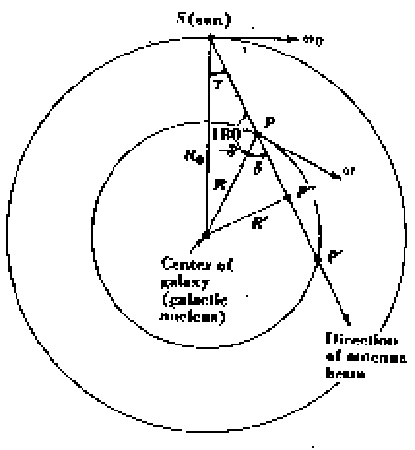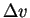
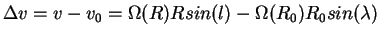The galactic disk indeed rotates differentially and this produces Doppler shifts in the observed spectral lines emitted from gas at different distances from the galactic center than the Sun. This is illustrated in fig 2.2. Once we measure the Doppler shift we can deduce the net velocity $\Delta v$

$$\Delta v= v - v_0 = \Omega (R) R sin(l) - \Omega(R_0) R_0 sin(\lambda)$$ (2.2)

but (see figure 2.3)

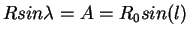$$R sin \lambda = A = R_0 sin(l)$$ (2.3)

and therefore:

$$\Delta v (R,l) = R_0 sin(l) [\Omega(R) - \Omega(R_0)]$$ (2.4)

Therefore if we know how the Galaxy rotational velocity depends on the distance from the center (that is, if we know the galactic rotational velocity curve, 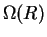$\Omega(R)$, see sec. 2.7) we can, for a given direction, associate at every radial velocity a distance along the line of sight.