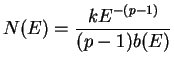Next: Cosmic Protons
Up: Cosmic Rays
Previous: Cosmic Rays
Contents
Assuming that the initial spectrum for cosmic ray electrons can be represented by a power law:
![$\displaystyle Q = k E^{-p} [electrons / cm^2 \; sec \; eV \; sr]$](img51.png) |
(1.3) |
the spectrum evolution follows the law :
![$\displaystyle \frac{dN}{dt} = D \nabla^{2} N + \frac{\partial}{\partial E} \left[ b(E) N(E)\right] + Q(E)$](img52.png) |
(1.4) |
where D is the diffusion coefficient and :
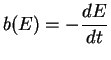 |
(1.5) |
Equation 1.4 can be resolved in first approximation by ignoring the terms
due to diffusion (assuming e.g. a uniform sources distribution) and
 /
/
 we obtain
we obtain
![$\displaystyle \frac{\partial}{\partial E} \left[ b(E) N(E)\right] = - Q (E) = -k E^{-p}$](img56.png) |
(1.6) |
and integrating :
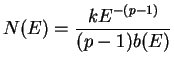 |
(1.7) |
The shape of the initial particle (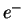 ) spectrum is therefore modified according to the dependence of
) spectrum is therefore modified according to the dependence of 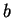 on
on 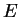 .
The energy loss can be due to:
.
The energy loss can be due to:
- Synchrotron losses: due to the interaction of electrons
with the galactic magnetic field and producing a radio emission
detectable in the MHz range. This energy loss is proportional to
the magnetic field energy density and to the square of the electron Lorentz factor.
For this reason the effect on N(E) is
especially important above a critical energy
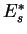 ,
causing, for E
,
causing, for E 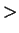
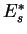 , N(E) to become
steeper and proportional to
, N(E) to become
steeper and proportional to
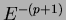
- Inverse Compton losses: they are due to the interaction with
the interstellar radiation field and with the cosmic background
radiation and produce emission in the gamma ray range (see par 1.5.3). As the
synchrotron losses, they are proportional to the square of the electrons
Lorentz factor and dominate at high energy. Also in this case the photon spectrum
becomes proportional to
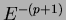 above a critical energy
above a critical energy 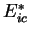 .
.
- Bremsstrahlung losses: they are due to interaction with the atomic
nuclei of the interstellar matter and produce gamma emission (see par. 1.5.2).
They are proportional to the electron energy and do not cause a change
in the electron spectral shape.
- Ionization losses: they are due to interaction with interstellar matter
atoms. They have a slight dependence on the electrons energy and the
spectrum become proportional to
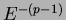
The radio observation of the synchrotron diffuse emission cover the range between few tens of MHz to a few GHz.
These observations show a radiation spectrum with index 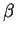 between 2.4 and 3, which corresponds to a spectral
index of the electron flux
between 2.4 and 3, which corresponds to a spectral
index of the electron flux 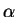 between 2 and 3.
In particular an increase of
between 2 and 3.
In particular an increase of 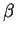 from 2.4-2.6 to 2.8-3 is observed for frequency larger than 400 MHz [Strong et al., 2000].
This can be connected to the spectral break due to synchrotron and inverse Compton energy losses, as is foreseen for electron spectrum at energy of about few GeV.
from 2.4-2.6 to 2.8-3 is observed for frequency larger than 400 MHz [Strong et al., 2000].
This can be connected to the spectral break due to synchrotron and inverse Compton energy losses, as is foreseen for electron spectrum at energy of about few GeV.
The spectrum of cosmic electrons can also be obtained from the direct measurements performed at the top of the atmosphere, for energies larger than some GeV, where the solar modulation is not important.
Recent measurements found that the local electron spectrum can be fitted by a single power-law, with index 3.4, up to 2-3 GeV [Casadei & Bindi, 2004].
However the electron distribution is expected to be very inhomogeneous for energies above some tens of GeV, as more energetic electrons are confined close to the sources [Strong et al., 2000], [Pohl & Esposito, 1998].
This suggests that the spectrum of cosmic electrons can be different from that measured locally.
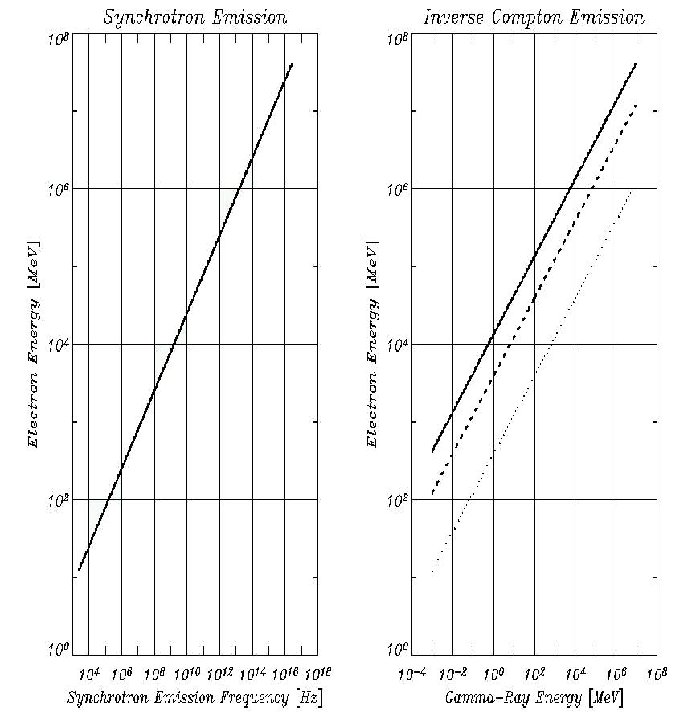
Figure 1.7:
Left: Relation between electron energy and frequency of the emitted synchrotron radiation, (a value of galactic magnetic field of 6 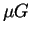 has been assumed).
Right: Relation between electron energy and energy of the emitted inverse-Compton radiation, for the stellar radiation field (dotted line), the dust radiation field (dashed line) and the cosmic microwave background (solid line)
has been assumed).
Right: Relation between electron energy and energy of the emitted inverse-Compton radiation, for the stellar radiation field (dotted line), the dust radiation field (dashed line) and the cosmic microwave background (solid line)
 |




Next: Cosmic Protons
Up: Cosmic Rays
Previous: Cosmic Rays
Contents
Andrea Giuliani
2005-01-21
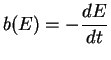
![$\displaystyle \frac{\partial}{\partial E} \left[ b(E) N(E)\right] = - Q (E) = -k E^{-p}$](img56.png)