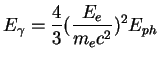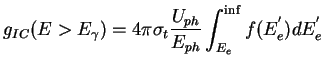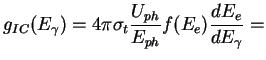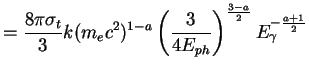Next: Modeling the Gamma-Ray Emission
Up: The physical processes producing
Previous: Electron Bremsstrahlung
Contents
Inverse Compton
The energy of a gamma photon produced via inverse Compton by an electron of energy 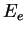 and a photon of energy
and a photon of energy 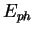 is:
is:
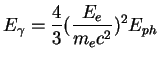 |
(1.23) |
The cross section of the reaction is the Thompson cross section (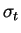 ). The inverse-Compton gamma-ray emissivity of interstellar matter is therefore:
). The inverse-Compton gamma-ray emissivity of interstellar matter is therefore:
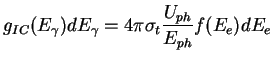 |
(1.24) |
where 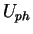 is the energy density of the radiation field of photons of energy
is the energy density of the radiation field of photons of energy 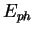 .
By integrating:
.
By integrating:
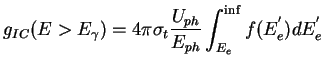 |
(1.25) |
where
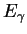 ,
, 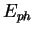 and
and 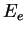 are related by eq. 1.23.
For a distribution of electrons with spectrum
are related by eq. 1.23.
For a distribution of electrons with spectrum
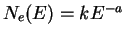 , from eq 1.24
, from eq 1.24 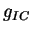 become:
become:
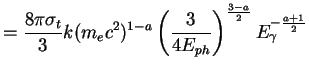 |
(1.26) |
Therefore the spectrum of produced photons is still a power law, with index
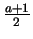




Next: Modeling the Gamma-Ray Emission
Up: The physical processes producing
Previous: Electron Bremsstrahlung
Contents
Andrea Giuliani
2005-01-21