



Next: L'angolo di apertura
Up: La materializzazione dei fotoni
Previous: La materializzazione dei fotoni
Contents
Si può definire una probabilità differenziale di produzione di coppia
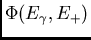 tale per cui
tale per cui 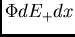 rappresenta la probabilità per un fotone di energia
rappresenta la probabilità per un fotone di energia 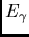 che
attraversa uno spessore
che
attraversa uno spessore 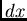
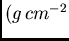 ) di produrre una coppia in cui
l'elettrone ha un'energia cinetica compresa tra
) di produrre una coppia in cui
l'elettrone ha un'energia cinetica compresa tra 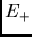 e
e 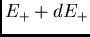 .
Assumendo che
.
Assumendo che
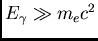 l'espressione teorica per
l'espressione teorica per 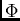 è :
è :
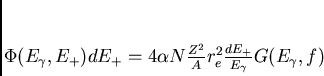 |
(2) |
dove
 |
(3) |
è la frazione di energia presa dal positrone e
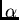 è la costante di struttura fine, N è il numero di Avogadro,
Z è il numero atomico, A è il numero di massa atomico e
è la costante di struttura fine, N è il numero di Avogadro,
Z è il numero atomico, A è il numero di massa atomico e
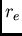 è il raggio dell'elettrone.
La funzione
è il raggio dell'elettrone.
La funzione
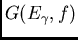 varia lentamente con
varia lentamente con 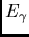 e
e 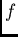 .
Il processo di creazione di coppie
dipende dall'intensità del campo elettrico nel punto in cui
avviene. Per questo, la sezione d'urto dipende, oltre che dall'energia del fotone
primario, dal numero atomico Z del materiale e dalla distanza dal nucleo.
Infatti, maggiore è questa distanza, maggiore sarà lo screening degli
elettroni orbitali. L'influenza dello screening è determinata dalla quantità :
.
Il processo di creazione di coppie
dipende dall'intensità del campo elettrico nel punto in cui
avviene. Per questo, la sezione d'urto dipende, oltre che dall'energia del fotone
primario, dal numero atomico Z del materiale e dalla distanza dal nucleo.
Infatti, maggiore è questa distanza, maggiore sarà lo screening degli
elettroni orbitali. L'influenza dello screening è determinata dalla quantità :
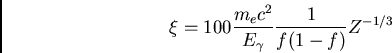 |
(4) |
. L'effetto di screening è
maggiore per uno 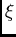 minore. Se
minore. Se 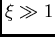 lo screeening è
trascurabile, mentre
lo screeening è
trascurabile, mentre 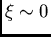 indica un completo screening. Per un dato
valore di
indica un completo screening. Per un dato
valore di 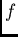 ,
, 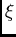 diminuisce all'aumentare di
diminuisce all'aumentare di 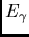 . Lo screening
può quindi essere considerato completo per ogni processo di produzione di
coppie quando l'energia dell'fotone incidente è grande (
. Lo screening
può quindi essere considerato completo per ogni processo di produzione di
coppie quando l'energia dell'fotone incidente è grande (
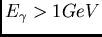 ).
).
Nei casi
limite di screening completo o di assenza di screening la funzione
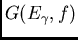 che appare nella (
che appare nella (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) vale
[Rossi, 1952]:
) vale
[Rossi, 1952]:
![\begin{displaymath}
G(E_{\gamma},f) = \left\{ \begin{array}{ll}
\left[f^2 + (...
...c^2}-\frac{1}{2}\right] & \xi \gg 1 \\
\end{array} \right.
\end{displaymath}](img74.png) |
(5) |
Essendo G simmetrica tra 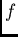 e
e 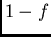 ,
, 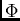 è complessivamente
simmetrica per l'elettrone e il positrone. Integrando
è complessivamente
simmetrica per l'elettrone e il positrone. Integrando 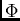 in
in
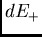 si ottiene la sezione d'urto totale, questo può essere fatto
analiticamente solo per i due casi limite:
si ottiene la sezione d'urto totale, questo può essere fatto
analiticamente solo per i due casi limite:
![\begin{displaymath}
\tau = \left\{ \begin{array}{ll}
4 \alpha N \frac{Z^2}{A}...
...\frac{109}{54}})\right] & \xi \gg 1 \\
\end{array} \right.
\end{displaymath}](img77.png) |
(6) |
Per valori intermedi di 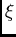 bisogna valutare l'integrale numericamente. Per
bisogna valutare l'integrale numericamente. Per
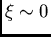 , e quindi per
, e quindi per 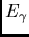 elevate,
elevate, 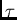 è circa
costante.
è circa
costante.
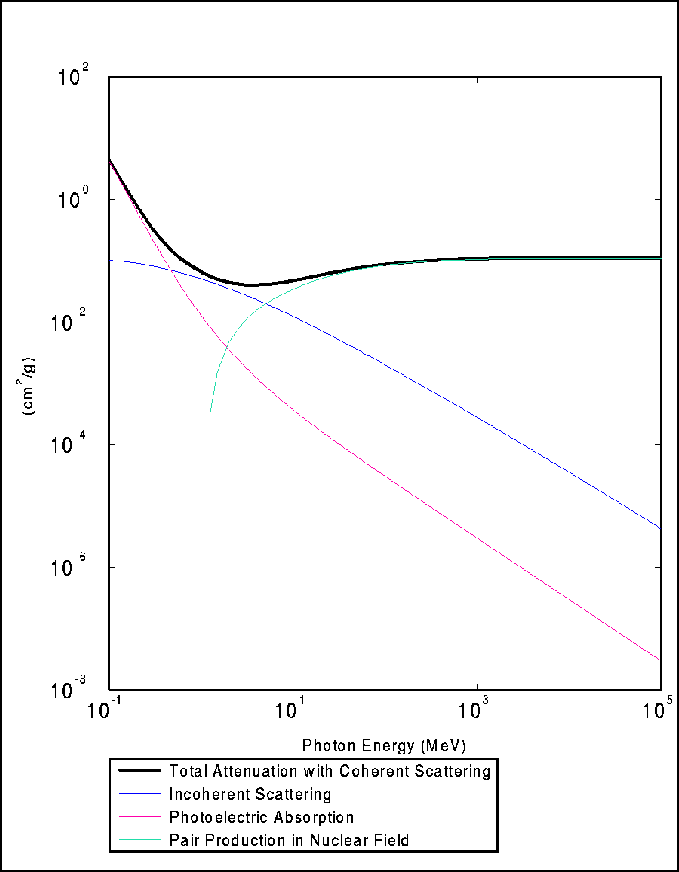
Figure:
Sezione d'urto del Tungsteno relativa ai principali processi di
perdita di energia per fotoni gamma. Per alte energie la produzione di coppie
domina sugli altri processi.
 |
La produzione di coppie può avvenire anche nel campo di un elettrone atomico.
La sezione d'urto che si ottiene da questa reazione è più piccola di
un fattore Z. Per tenere conto di questa interazione si puo' quindi sostituire
nella formula precedente 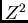 con Z(Z+1).
con Z(Z+1).
In figura ![[*]](file:/usr/lib/latex2html/icons/crossref.png) è mostrata la sezione d'urto totale relativa al
Tungsteno per
la produzione di coppie in funzione di
è mostrata la sezione d'urto totale relativa al
Tungsteno per
la produzione di coppie in funzione di 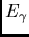 e in relazione agli altri
principali processi di
assorbimento, lo scattering Compton e fotoelettrico. Al di sopra dell'energia di
soglia la probabilità di assorbimento di un fotone per produzione di coppie
aumenta molto velocemente, fino a diventare il processo dominante per energie
maggiori di circa 10 MeV.
e in relazione agli altri
principali processi di
assorbimento, lo scattering Compton e fotoelettrico. Al di sopra dell'energia di
soglia la probabilità di assorbimento di un fotone per produzione di coppie
aumenta molto velocemente, fino a diventare il processo dominante per energie
maggiori di circa 10 MeV.
E' interessante studiare come l'energia del fotone si divida tra i due elettroni
prodotti, questa informazione è contenuta in 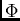 . In figura
. In figura
![[*]](file:/usr/lib/latex2html/icons/crossref.png) è graficata
è graficata 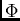 in funzione di
in funzione di 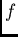 per diverse
per diverse
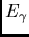 . Va notato che il valore di
. Va notato che il valore di 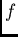 più probabile varia al variare
dell'energia del fotone incidente, in particolare per alte energie è favorita
una ripartizione asimmetrica dell'energia.
più probabile varia al variare
dell'energia del fotone incidente, in particolare per alte energie è favorita
una ripartizione asimmetrica dell'energia.
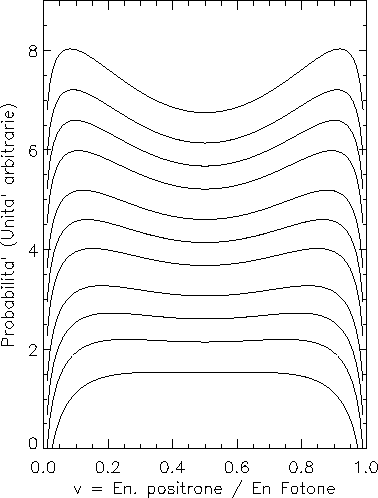
Figure:
Probabilità di reazione in funzione della distribuzione di energia
tra gli elettroni secondari.
 |




Next: L'angolo di apertura
Up: La materializzazione dei fotoni
Previous: La materializzazione dei fotoni
Contents
Andrea Giuliani
2003-10-14
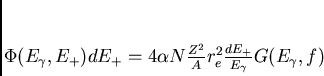

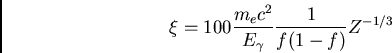
![\begin{displaymath}
G(E_{\gamma},f) = \left\{ \begin{array}{ll}
\left[f^2 + (...
...c^2}-\frac{1}{2}\right] & \xi \gg 1 \\
\end{array} \right.
\end{displaymath}](img74.png)
![\begin{displaymath}
\tau = \left\{ \begin{array}{ll}
4 \alpha N \frac{Z^2}{A}...
...\frac{109}{54}})\right] & \xi \gg 1 \\
\end{array} \right.
\end{displaymath}](img77.png)

