Neutrini da SN 1987A¶
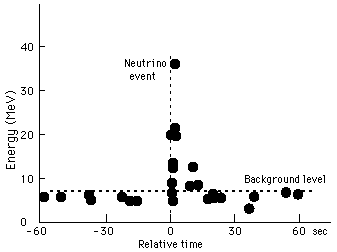
Associati all'evento SN 1987A sono stati osservati 12 neutrini di energia ~20 MeV con un tempo di arrivo compatibile con un ritardo minore di 1 giorno rispetto al segnale luminoso.
- Che neutrini sono stati osservati?
- cosa possiamo dire della loro massa ?
- quanto vale l'area di raccolta di Kamiokande ?
In [1]:
delay = 3600.*24 # sec
dist = 50e3 * 3e18 # cm
c = 3e10 # cm/s
Calcoliamo il tempo di viaggio dei fotoni :
In [2]:
t_fot = dist / c
print('Tempo di viaggio fotoni [s]' , t_fot )
print('Tempo di viaggio fotoni [yrs]', t_fot /3e7 )
Calcoliamo $\beta_{\nu} = v_{\nu} / c$
In [3]:
t_nu = t_fot + delay # tempo di viaggio dei neutrini [s]
v_nu = dist / t_nu # velocita' dei neutrini [cm/s]
beta = v_nu / c # beta dei neutrini
print(beta)
Calcoliamo $\gamma_{\nu} = 1 / \sqrt{1 - \beta_{\nu}^2}$
In [4]:
gamma = 1. / sqrt(1-beta**2.)
print (gamma)
La massa del neutrino sara' quindi :
$m_{\nu} \simeq E_{\nu} / \gamma_{\nu} $
In [5]:
m0 = 20e6 / gamma
print( 'Massa [eV] <', m0 )
Assumiamo 1.4 $M_{\odot}$ come massa totale dei neutroni che si sono formati nell'evento. Il numeri di neutrino emessi sara' quindi:
In [6]:
L = 1.4 * 2e33 / 1.67e-24
print(L)
In [7]:
f = L / (4*3.14*dist**2.)
print('Flusso di neutrini [cm-2]',f)
In [20]:
A = 12 / f
print ('Area di raccolta [cm2] ',A)