Vogliamo calcolare la Mass Function del sistema (Eg.1) :
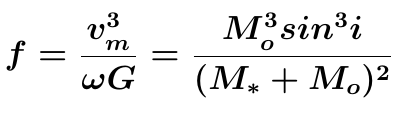
In [8]:
from numpy import *
from astropy import units as u
from astropy.constants import G
Iniziamo convertendo in unita' cgs la velocita' radiale della stella :
In [41]:
vm = 156 *1e5 *u.cm/u.s
print(vm)
Calcoliamo la frequenza angolare dell'orbita
In [15]:
period = 5.6 *24 *3600. *u.s # Periodo in secondi
omega = 2 * pi / period
print(omega)
Ora possiamo calcolare la Mass Function
In [42]:
massFunction = vm**3. / ( G.cgs * omega )
print(massFunction)
print(massFunction.to('solMass'))
Ora cerchiamo graficamente quali sono i valori di M0 e inclinazione dell'orbita che danno una Mass Function uguale a ~ 2.2 masse solari.
Plottiamo quindi il secondo termine dell'Eq.1 per diversi valori di M0 e i (M* sappiamo che vale 30 masse solari.)
In [40]:
mst = 30. * u.solMass
ii = arange(90,0,-20) *u.deg # Possibili inclinazioni dell'orbita
m0 = logspace(0,2) * u.solMass # Possibili valori della massa dell'oggetto compagno
for i in ii :
mf = ( m0*sin(i) )**3. / (m0 + mst)**2. # Mass Function
plot( m0, mf, label=str(i) )
hlines(massFunction.to_value('solMass'),1e0,1e2,linestyle='--')
xlabel('$M_{o}$ [s.m.]')
ylim([1e-1,5e1]) ; ylabel('Mass Function [s.m.]')
loglog() ; legend()
Out[40]:
L'oggetto companio e' quindi un buco nero.